Le processus ponctuel de Poisson est un processus stochastique d'un type un
peu différent, qui associe une distribution de probabilité aux
configurations de points sur 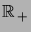 . Ces points modélisent, par exemple,
les temps de passage d'un bus à un arrêt, les instants d'arrivée
d'appels téléphoniques dans une centrale, et ainsi de suite.
. Ces points modélisent, par exemple,
les temps de passage d'un bus à un arrêt, les instants d'arrivée
d'appels téléphoniques dans une centrale, et ainsi de suite.
Le processus peut être caractérisé de plusieurs manières
différentes. Une réalisation peut être spécifiée par une suite
croissante de nombres réels positifs
Supposant qu'un tel processus existe bel et bien, nous pouvons dériver
quelques-unes de ses propriétés.
La propriété remarquable du processus de Poisson est alors que les
variables aléatoires
![$ N_{]t,t+s]}$](img568.png) suivent nécessairement une loi de
Poisson de paramètre
suivent nécessairement une loi de
Poisson de paramètre 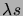 .
.
D´EMONSTRATION.
Par la propriété 1., il suffit de montrer le résultat pour

,
c'est-à-dire pour
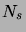
. Partageons
![$ ]0,s]$](img573.png)
en
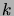
intervalles de longueur
égale, de la forme
L'idée de la preuve est que pour
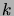
suffisamment grand, il est peu
probable d'avoir plus d'un point par intervalle, donc la loi de
![$ Y^{(k)}_j
= N_{]s_{j-1},s_j]}$](img577.png)
est à peu près une loi de Bernoulli. La loi de
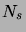
est donc proche d'une loi binomiale, que l'on peut approximer par la
loi de Poisson pour
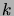
grand.
Il suit des conditions 1. et 2. que les  sont i.i.d.,
de même loi que
sont i.i.d.,
de même loi que
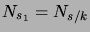 , et on a
, et on a
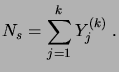 |
(3.27) |
Introduisons alors des variables aléatoires
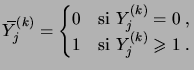 |
(3.28) |
Les
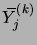
sont également i.i.d.. La variable aléatoire
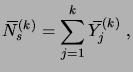 |
(3.29) |
satisfaisant
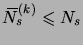
pour tout
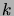
, on a
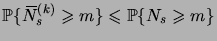 |
(3.30) |
pour tout
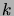
et tout
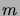
. De plus,
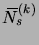
suit une loi
binomiale de paramètre
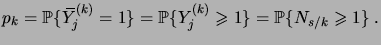 |
(3.31) |
Estimons maintenant la différence entre les lois de
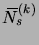
et
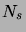
. Nous avons
La condition 5. avec
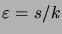
implique alors
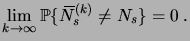 |
(3.33) |
Comme on a d'une part la minoration
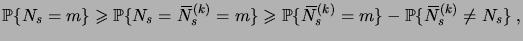 |
(3.34) |
et d'autre part la majoration
il suit que
 |
(3.36) |
Il reste à montrer que

tend vers
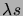
pour
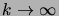
. Si
c'est le cas, alors la Proposition
1.6.3 montre que
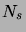
suit une
loi de Poisson de paramètre
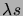
.
Or nous avons
Un calcul analogue montre que
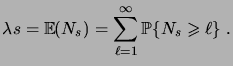 |
(3.38) |
Il suit de (
3.2.10) que
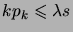
pour tout
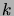
.
Par un théorème d'analyse, on peut alors intervertir limite et somme, et
écrire
 |
(3.39) |
en vertu de (
3.2.16). Ceci montre que

converge bien vers
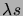
, et par conséquent que la loi de
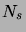
, étant la limite
d'une loi binomiale de paramètre

, est une loi de Poisson de
paramètre
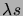
.

La seconde construction du processus ponctuel de Poisson se base sur la
distribution des différences de position
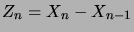 . Celles-ci
caractérisent également de manière univoque le processus, via la
relation
. Celles-ci
caractérisent également de manière univoque le processus, via la
relation
D´EMONSTRATION.
Fixons des instants
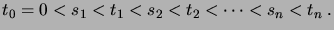 |
(3.41) |
Nous pouvons alors calculer
La loi conjointe de

admet donc la densité
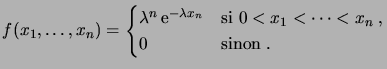 |
(3.43) |
Nous pouvons alors calculer la fonction de répartion des

:
La densité conjointe de

s'obtient alors en calculant la
dérivée
Or cette densité est bien la densité conjointe de
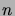
variables
exponentielles indépendantes de paramètre
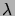
.

Ce résultat fournit une méthode permettant de construire le processus de
Poisson: chaque 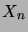 est obtenu à partir de
est obtenu à partir de 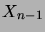 en lui ajoutant une
variable aléatoire de loi exponentielle, indépendante des variables
précédentes. Ceci présuppose l'existence d'un espace probabilisé
pouvant contenir une infinité de variables aléatoires exponentielles
indépendantes: C'est l'espace produit que nous avons évoqué (sans
prouver son existence) dans l'Exemple 2.3.4.
en lui ajoutant une
variable aléatoire de loi exponentielle, indépendante des variables
précédentes. Ceci présuppose l'existence d'un espace probabilisé
pouvant contenir une infinité de variables aléatoires exponentielles
indépendantes: C'est l'espace produit que nous avons évoqué (sans
prouver son existence) dans l'Exemple 2.3.4.
![]() . Ces points modélisent, par exemple,
les temps de passage d'un bus à un arrêt, les instants d'arrivée
d'appels téléphoniques dans une centrale, et ainsi de suite.
. Ces points modélisent, par exemple,
les temps de passage d'un bus à un arrêt, les instants d'arrivée
d'appels téléphoniques dans une centrale, et ainsi de suite.
![]() suivent nécessairement une loi de
Poisson de paramètre
suivent nécessairement une loi de
Poisson de paramètre ![]() .
.
![]() sont i.i.d.,
de même loi que
sont i.i.d.,
de même loi que
![]() , et on a
, et on a
![]() . Celles-ci
caractérisent également de manière univoque le processus, via la
relation
. Celles-ci
caractérisent également de manière univoque le processus, via la
relation
![]() est obtenu à partir de
est obtenu à partir de ![]() en lui ajoutant une
variable aléatoire de loi exponentielle, indépendante des variables
précédentes. Ceci présuppose l'existence d'un espace probabilisé
pouvant contenir une infinité de variables aléatoires exponentielles
indépendantes: C'est l'espace produit que nous avons évoqué (sans
prouver son existence) dans l'Exemple 2.3.4.
en lui ajoutant une
variable aléatoire de loi exponentielle, indépendante des variables
précédentes. Ceci présuppose l'existence d'un espace probabilisé
pouvant contenir une infinité de variables aléatoires exponentielles
indépendantes: C'est l'espace produit que nous avons évoqué (sans
prouver son existence) dans l'Exemple 2.3.4.