



Next: Fonction génératrice
Up: Probabilités discrètes
Previous: Théorème de la limite
Contents
Loi de Poisson et `` loi des petits nombres''
La loi normale donne une bonne approximation de la loi binomiale pour  fixé et
fixé et 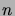 tendant vers l'infini. La loi de Poisson, quant à elle,
décrit bien la loi binomiale pour
tendant vers l'infini. La loi de Poisson, quant à elle,
décrit bien la loi binomiale pour 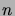 tendant vers l'infini et
tendant vers l'infini et  tendant vers zéro, avec le produit
tendant vers zéro, avec le produit 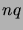 tendant vers une constante. Elle
modélise donc les expériences de Bernoulli avec une très faible
probabilité de succès, mais avec un grand nombre d'essais, du même
ordre de grandeur que l'inverse de la probabilité de succès.
tendant vers une constante. Elle
modélise donc les expériences de Bernoulli avec une très faible
probabilité de succès, mais avec un grand nombre d'essais, du même
ordre de grandeur que l'inverse de la probabilité de succès.
![\begin{definition}[Loi de Poisson]
La\/ \defwd{loi de Poisson}\/ de param\\lq etre\...
...bda}\frac{\lambda^k}{k!}
\qquad
\forall k\in\N\;.
\end{equation}\end{definition}](img198.png)
Remarquons que
 définit bien une loi de probabilité,
puisque
définit bien une loi de probabilité,
puisque
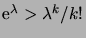 pour tout
pour tout 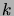 et donc
et donc
![$ \pi_\lambda(k)\in[0,1]$](img201.png) , et
, et
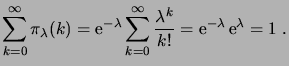 |
(1.38) |

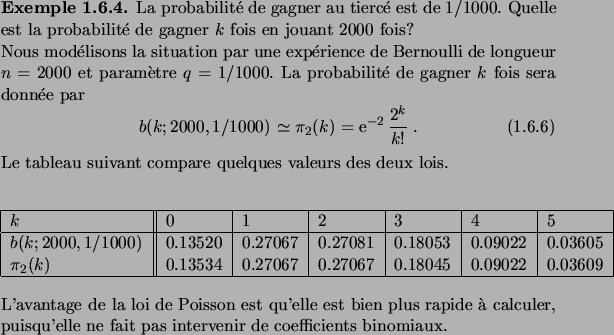
D´EMONSTRATION.


La proposition suivante établit la convergence (simple, c'est-à-dire
à  fixé) de la loi binomiale vers la loi de Poisson.
fixé) de la loi binomiale vers la loi de Poisson.
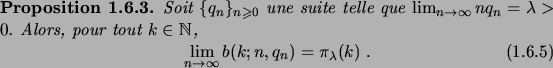
D´EMONSTRATION.
Soit
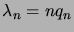
. Alors
Lorsque

, on a
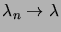
,
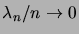
et
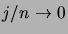
pour

, donc
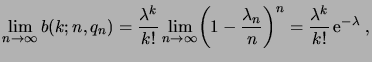 |
(1.40) |
la dernière égalité pouvant se montrer par un développement limité de
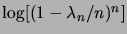
.

On peut en fait faire beaucoup mieux que de montrer la convergence simple de
la loi binomiale vers la loi de Poisson, et borner la `` distance
 '' entre les deux lois.
'' entre les deux lois.
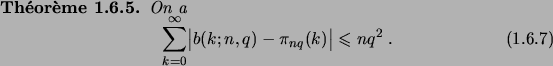
D´EMONSTRATION.
La démonstration que nous allons donner est une petite merveille de la
théorie des probabilités. Elle n'utilise pratiquement pas d'analyse,
mais un grand nombre de concepts de probabilités discrètes vus
jusqu'ici.
Nous commençons par introduire des espaces probabilisés
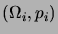 , pour
, pour
 , donnés par
, donnés par
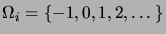 et
et
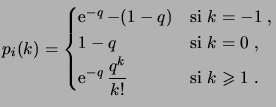 |
(1.41) |
On vérifiera que les
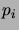
définissent bien une distribution de
probabilité. Sur chaque
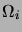
, nous introduisons les deux variables
aléatoires
 |
(1.42) |
De cette manière, on a

,
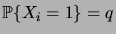
,
et
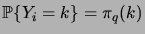
pour tout
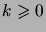
. De plus,
donc
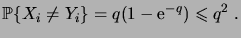 |
(1.44) |
Soit
l'espace produit des
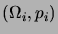
. Alors

Comme
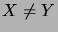
implique que
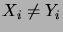
pour un
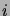
au moins, il suit
de (
1.6.14) que
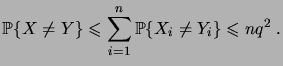 |
(1.45) |
Il reste donc à montrer que la le membre de gauche de (
1.6.10) est
majoré par

. Un tel procédé s'appelle un argument de
couplage. Nous posons, pour abréger l'écriture,

,
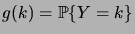
et

. Alors
Or nous pouvons écrire
ce qui conclut la démonstration.

Le corollaire suivant montre l'utilité de la relation (1.6.10).

D´EMONSTRATION.
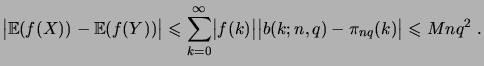 |
(1.48) |
La relation (
1.6.19) est un cas particulier de (
1.6.18), avec
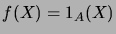
égale à la fonction indicatrice de
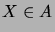
. En
effet, on a
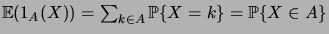
et
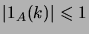
pour tout

.






Next: Fonction génératrice
Up: Probabilités discrètes
Previous: Théorème de la limite
Contents
berglund
2005-11-28
![]() fixé et
fixé et ![]() tendant vers l'infini. La loi de Poisson, quant à elle,
décrit bien la loi binomiale pour
tendant vers l'infini. La loi de Poisson, quant à elle,
décrit bien la loi binomiale pour ![]() tendant vers l'infini et
tendant vers l'infini et ![]() tendant vers zéro, avec le produit
tendant vers zéro, avec le produit ![]() tendant vers une constante. Elle
modélise donc les expériences de Bernoulli avec une très faible
probabilité de succès, mais avec un grand nombre d'essais, du même
ordre de grandeur que l'inverse de la probabilité de succès.
tendant vers une constante. Elle
modélise donc les expériences de Bernoulli avec une très faible
probabilité de succès, mais avec un grand nombre d'essais, du même
ordre de grandeur que l'inverse de la probabilité de succès.
![]() définit bien une loi de probabilité,
puisque
définit bien une loi de probabilité,
puisque
![]() pour tout
pour tout ![]() et donc
et donc
![]() , et
, et
![]() fixé) de la loi binomiale vers la loi de Poisson.
fixé) de la loi binomiale vers la loi de Poisson.
![]() '' entre les deux lois.
'' entre les deux lois.
![]() , pour
, pour
![]() , donnés par
, donnés par
![]() et
et
