



Next: Mesures de probabilité et
Up: Probabilités continues
Previous: Variables aléatoires réelles à
Contents
Vecteurs aléatoires à densité
![\begin{definition}[Vecteur al\'eatoire]
On appelle\/ \defwd{vecteur al\'eatoire}...
...n)$\ o\\lq u chaque $X_i$\ est une variable al\'eatoire r\'eelle.
\end{definition}](img322.png)
Nous aimerions associer, quand c'est possible, une densité
 à un tel vecteur aléatoire. C'est-à-dire que la
probabilité que
à un tel vecteur aléatoire. C'est-à-dire que la
probabilité que 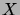 appartienne à un sous-ensemble
appartienne à un sous-ensemble
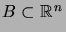 devrait pouvoir s'écrire comme une intégrale multiple de
devrait pouvoir s'écrire comme une intégrale multiple de 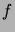 sur
sur 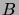 .
.
Considérons d'abord le cas  . Supposons que pour une fonction
. Supposons que pour une fonction
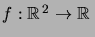 , l'intégrale
, l'intégrale
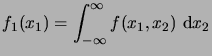 |
(2.4) |
existe pour chaque 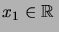 . Supposons de plus que la fonction
. Supposons de plus que la fonction 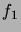 est
intégrable. Le théorème de Fubini affirme que l'intégrale de
est
intégrable. Le théorème de Fubini affirme que l'intégrale de 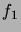 est égale à celle de
est égale à celle de
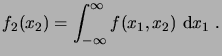 |
(2.5) |
On note alors
 |
(2.6) |
Si
 , on introduit de plus
, on introduit de plus
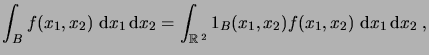 |
(2.7) |
pour autant que cette dernière intégrale existe, où
 |
(2.8) |
désigne la fonction indicatrice de 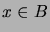 .
Ces notations se généralisent à des fonctions
.
Ces notations se généralisent à des fonctions
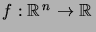 .
.
![\begin{definition}[Densit\'e d'un vecteur al\'eatoire]
Une fonction int\'egrable...
...\'e conjointe} des variables al\'eatoires $X_1$, \dots, $X_n$.
\end{definition}](img335.png)
Le théorème suivant, sur lequel nous reviendrons dans la section
suivante, permet d'étendre la relation (2.2.7) à des
événements plus généraux. Pour l'instant il suffira de savoir que
les Boréliens sont une classe de sous-ensembles de  ,
comprenant en particulier les ouverts et les fermés de
,
comprenant en particulier les ouverts et les fermés de 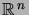 , ainsi que
toutes leurs réunions et intersections.
, ainsi que
toutes leurs réunions et intersections.
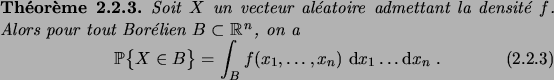


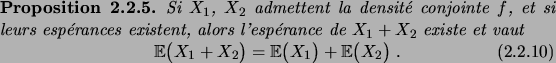
D´EMONSTRATION.
En utilisant (
2.2.15) et le changement de variable
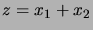
, on a

![\begin{definition}[Ind\'ependance]
Les variables al\'eatoires r\'eelles $X_1,\do...
... a_n}
\end{equation}pour tout choix de $a_1, \dots, a_n\in\R$.
\end{definition}](img349.png)
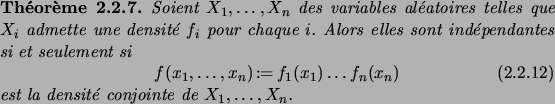
D´EMONSTRATION.
![\begin{itemiz}
\item[$\Leftarrow$] Si $f$\ est la densit\'e de $X$, alors
\begin...
...(x_1,\dots,x_n)$\ est la densit\'e conjointe de $(X_1,\dots,X_n)$.
\end{itemiz}](img351.png)

Remarquons que les 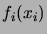 sont évidemment les densités marginales
de
sont évidemment les densités marginales
de
 . La relation (2.2.13) implique immédiatement
le résultat suivant.
. La relation (2.2.13) implique immédiatement
le résultat suivant.
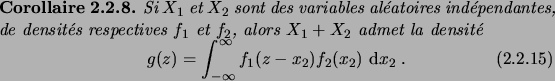
Ceci motive la définition suivante.
![\begin{definition}[Convolution]
Si $f_1$\ et $f_2$\ sont deux densit\'es, la fon...
...ation}s'appelle la\/ \defwd{convolution}\/ de $f_1$\ et $f_2$.
\end{definition}](img354.png)
Nous appliquons maintenant ces résultats au cas particulier important
de variables aléatoires gaussiennes, c'est-à-dire suivant des lois
normales.

D´EMONSTRATION.
Nous allons considérer le cas

, le cas général s'en déduit par
récurrence. Il est plus commode de travailler avec
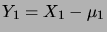
et
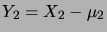
, qui suivent des lois normales centrées (c'est-à-dire
de moyenne nulle). Soit
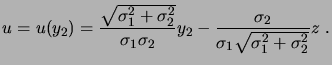 |
(2.10) |
Nous allons utiliser le fait que
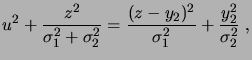 |
(2.11) |
qui se vérifie par un calcul élémentaire.
La densité
de
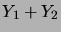
est alors donnée par la convolution
où nous avons utilisé le changement de variable
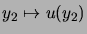
. Ceci
montre que
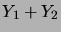
suit la loi

, et par
conséquent
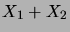
suit la loi
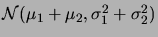
.

La densité conjointe des 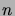 variables gaussiennes indépendantes est donnée
par
variables gaussiennes indépendantes est donnée
par
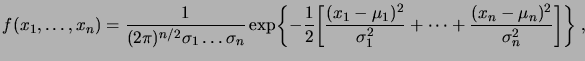 |
(2.13) |
on l'appelle une densité gaussienne à 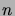 dimensions. Considérons le
cas où les
dimensions. Considérons le
cas où les 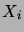 suivent la loi normale standard, c'est-à-dire
suivent la loi normale standard, c'est-à-dire
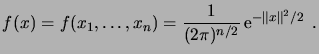 |
(2.14) |
Par l'indépendance, nous aurons
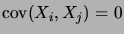 pour
pour 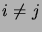 , alors
que
, alors
que
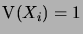 , et par conséquent
, et par conséquent
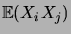 vaut
vaut 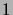 si
si 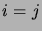 ,
0 sinon. Soit alors
,
0 sinon. Soit alors 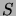 une matrice non singulière, c'est-à-dire
telle que
une matrice non singulière, c'est-à-dire
telle que
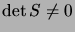 , et
, et 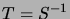 . Considérons la variable
aléatoire
. Considérons la variable
aléatoire
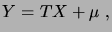 |
(2.15) |
dont l'espérance vaut 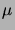 . Quelle est sa densité? Nous avons, en vertu
de la formule de changement de variable,
. Quelle est sa densité? Nous avons, en vertu
de la formule de changement de variable,
Par conséquent, la densité de 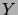 est donnée par
est donnée par
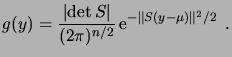 |
(2.17) |
Remarquons que l'on peut récrire
où 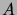 est la matrice symétrique définie positive
est la matrice symétrique définie positive  ,
d'éléments
,
d'éléments 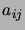 , qui satisfait
, qui satisfait
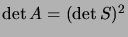 . Nous avons
donc
. Nous avons
donc
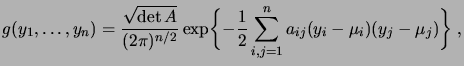 |
(2.19) |
qui est la forme générale d'une densité gaussienne. Nous avons
déjà vu que son espérance vaut 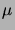 . Quant à sa covariance, elle se
calcule en observant que
. Quant à sa covariance, elle se
calcule en observant que
d'où, comme
 ,
,
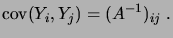 |
(2.21) |
La matrice 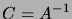 s'appelle la matrice de covariance de la
densité gaussienne (2.2.32). Nous voyons en particulier que les
variables
s'appelle la matrice de covariance de la
densité gaussienne (2.2.32). Nous voyons en particulier que les
variables
 sont non corrélées si et seulement si
sont non corrélées si et seulement si 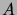 est
diagonale, ce qui est le cas si et seulement si les variables sont
indépendantes.
est
diagonale, ce qui est le cas si et seulement si les variables sont
indépendantes.
![\begin{definition}[Densit\'e gaussienne]
Soit $C$\ une matrice $n\times n$\ sym\...
... gaussienne de moyenne $\mu$\ et matrice de
covariance $C$}\/.
\end{definition}](img401.png)
Voici pour terminer une autre propriété remarquable des densités
gaussiennes.
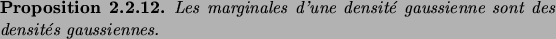
D´EMONSTRATION.
Il suffit à nouveau de considérer le cas

,
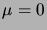
, les cas de
dimension plus élevée pouvant être traités par récurrence. Or
l'identité
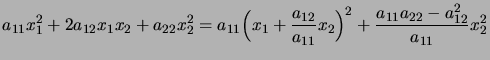 |
(2.22) |
permet d'effectuer l'intégrale de la densité sur
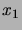
, à l'aide du
changement de variable
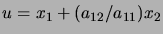
. La densité marginale
est donc proportionnelle à
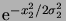
, avec
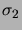
donné par
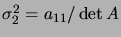
.





Next: Mesures de probabilité et
Up: Probabilités continues
Previous: Variables aléatoires réelles à
Contents
berglund
2005-11-28
![\begin{definition}[Vecteur al\'eatoire]
On appelle\/ \defwd{vecteur al\'eatoire}...
...n)$\ o\\lq u chaque $X_i$\ est une variable al\'eatoire r\'eelle.
\end{definition}](img322.png)
![]() à un tel vecteur aléatoire. C'est-à-dire que la
probabilité que
à un tel vecteur aléatoire. C'est-à-dire que la
probabilité que ![]() appartienne à un sous-ensemble
appartienne à un sous-ensemble
![]() devrait pouvoir s'écrire comme une intégrale multiple de
devrait pouvoir s'écrire comme une intégrale multiple de ![]() sur
sur ![]() .
.
![]() . Supposons que pour une fonction
. Supposons que pour une fonction
![]() , l'intégrale
, l'intégrale
![]() ,
comprenant en particulier les ouverts et les fermés de
,
comprenant en particulier les ouverts et les fermés de ![]() , ainsi que
toutes leurs réunions et intersections.
, ainsi que
toutes leurs réunions et intersections.
![]() sont évidemment les densités marginales
de
sont évidemment les densités marginales
de
![]() . La relation (2.2.13) implique immédiatement
le résultat suivant.
. La relation (2.2.13) implique immédiatement
le résultat suivant.
![]() variables gaussiennes indépendantes est donnée
par
variables gaussiennes indépendantes est donnée
par