Fonction génératrice

Nous terminons cette première partie en introduisant la notion de fonction génératrice, qui est un outil permettant de simplifier le calcul d'espérances.

$\begin{definition}[Fonction g\'en\'eratrice] Soit $X$\ une variable al\'eatoire ... ...uation} G_X(z) = \sum_{k\geqs 0}z^k \prob{X=k}\;. \end{equation}\end{definition}$

$\displaystyle G'_X(z)$	$\displaystyle = \sum_{k\geqs 0}kz^{k-1} \prob{X=k}$	$\displaystyle \Rightarrow$	$\displaystyle G'_X(1)$	$\displaystyle = \sum_{k\geqs 0}k \prob{X=k} = \expec{X}\;,$
$\displaystyle G''_X(z)$	$\displaystyle = \sum_{k\geqs 0}k(k-1)z^{k-2} \prob{X=k}$	$\displaystyle \Rightarrow$	$\displaystyle G''_X(1)$	$\displaystyle = \sum_{k\geqs 0}k(k-1) \prob{X=k}$
				$\displaystyle = \expec{X(X-1)}\;.$	(1.50)

$\begin{prop} Soit $X$\ une variable al\'eatoire \\lq a valeurs dans $\N$\ dont la f... ...G'_X(1)\;,\\ \Var(X) &= G''_X(1) + G'_X(1) - G'_X(1)^2\;. \end{align}\end{prop}$

$\begin{example}\hfill \begin{enum} \item \defwd{Loi g\'eom\'etrique:}\/ $\prob... ...;. \end{equation} Le rayon de convergence est infini. \end{enum}\end{example}$

On vérifiera que les relations (1.7.4) donnent bien les espérances et les variances calculées précédemment. Nous les résumons dans le tableau suivant.

Loi	$\prob{X=k}$		$\expec{X}$	$\Var(X)$
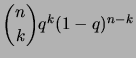$\begin{displaymath}\begin{array}{c} \text{Binomiale} \\ b(k; n,q) \end{array}\end{displaymath}$	$\dbinom nk q^k (1-q)^{n-k}$	$\bigpar{qz + 1-q}^n$
$\begin{displaymath}\begin{array}{c} \text{G\'eom\'etrique} \end{array}\end{displaymath}$	$q (1-q)^{k-1}$	$\dfrac{qz}{1-(1-q)z}$	$\dfrac1q$	$\dfrac{1-q}{q^2}$
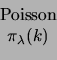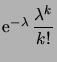$\begin{displaymath}\begin{array}{c} \text{Poisson} \\ \pi_\lambda(k) \end{array}\end{displaymath}$	$\e^{-\lambda}\dfrac{\lambda^k}{k!}$	$\e^{\lambda(z-1)}$	$\lambda$	$\lambda$

Finalement, le résultat suivant permet, en particulier, de retrouver des résultats que nous avons déjà dérivés pour l'espérance de la somme de certaines variables aléatoires.

$\begin{prop} Si $X$\ et $Y$\ sont ind\'ependantes, \\lq a valeurs dans $\N$, avec fonctions g\'en\'eratrices $G_X$\ et $G_Y$, alors $G_{X+Y}=G_XG_Y$. \end{prop}$

D´EMONSTRATION. On a

$\displaystyle G_{X+Y}(z)$	$\displaystyle = \sum_{k\geqs 0} z^k \prob{X+Y=k}$
	$\displaystyle = \sum_{k\geqs 0} \sum_{\ell=0}^k z^k \prob{X=\ell, Y=k-\ell}$
	$\displaystyle = \sum_{k\geqs 0} \sum_{\ell=0}^k z^k \prob{X=\ell}\prob{Y=k-\ell}$
	$\displaystyle = \sum_{\ell\geqs 0} \sum_{n\geqs 0}^{\phantom{k}} z^{\ell+n} \prob{X=\ell}\prob{Y=n}$
	$\displaystyle = G_X(z) G_Y(z)\;.$	(1.51)

$\qedsymbol$

On remarquera en particulier que la somme de deux variables aléatoires de loi binomiale suit encore une loi binomiale, et que la somme de deux variables aléatoires de loi de Poisson suit encore une loi de Poisson, comme nous l'avons montré précédemment.