



Next: Loi de Poisson et
Up: Probabilités discrètes
Previous: Loi des grands nombres
Contents
Théorème de la limite centrale
Dans cette section, nous allons donner une interprétation plus précise
de la variance d'une variable aléatoire. Examinons à nouveau la somme
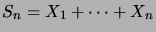 de
de 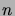 variables aléatoires de même espérance
variables aléatoires de même espérance
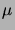 et même variance
et même variance  . Nous supposerons les
. Nous supposerons les 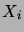 indépendants. Nous avons vu dans la section précédente que la
moyenne
indépendants. Nous avons vu dans la section précédente que la
moyenne 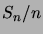 a une grande probabilité d'être proche de
a une grande probabilité d'être proche de 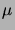 , mais
comment se comporte l'écart
, mais
comment se comporte l'écart
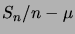 ? Dans la preuve du
Théorème 1.4.3, nous avons vu que
? Dans la preuve du
Théorème 1.4.3, nous avons vu que
 |
(1.13) |
Le membre de droite tend vers zéro lorsque
 , non seulement
pour
, non seulement
pour 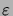 constant, mais également si
constant, mais également si
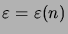 satisfait
satisfait
 . Par contre, il reste constant si
. Par contre, il reste constant si
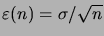 . On dit que la moyenne
. On dit que la moyenne 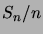 `` se
concentre'' dans un intervalle
`` se
concentre'' dans un intervalle
![$ [\mu-\sigma/\sqrt n, \mu+\sigma/\sqrt
n\,]$](img125.png) . Pour étudier plus précisément la déviation entre la moyenne et
l'espérance, on introduit la variable rééchelonnée
. Pour étudier plus précisément la déviation entre la moyenne et
l'espérance, on introduit la variable rééchelonnée
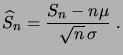 |
(1.14) |
Remarquons que
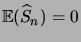 et
et
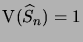 .
.
Le théorème de la limite centrale affirme que pour tout
intervalle
![$ [a,b]\subset\R$](img129.png) ,
,
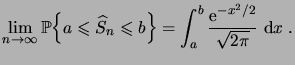 |
(1.15) |
Commençons par vérifier que le membre de droite définit bien une
probabilité.

D´EMONSTRATION.
L'astuce consiste à calculer le carré de l'intégrale, qui vaut
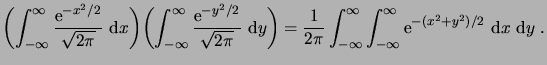 |
(1.16) |
En passant en coordonnées polaires
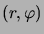
, et tenant compte du
Jacobien de la transformation
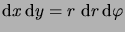
,
cette expression devient
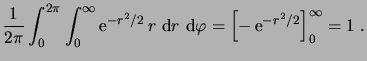 |
(1.17) |

On a donc bien
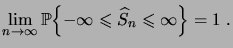 |
(1.18) |
Pour démontrer le théorème de la limite centrale dans le cas
particulier de la loi binomiale
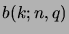 , il est utile de connaître la formule de Stirling:
, il est utile de connaître la formule de Stirling:
![\begin{lemma}[Formule de Stirling]
\begin{equation}
\lim_{n\to\infty} \frac{n!}{n^n \e^{-n} \sqrt{2\pi n}} = 1\;.
\end{equation}\end{lemma}](img138.png)
D´EMONSTRATION.
Considérons la fonction Gamma d'Euler
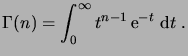 |
(1.19) |
Il est clair que
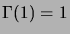
, et une intégration par parties montre que
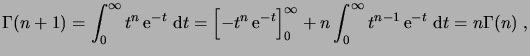 |
(1.20) |
d'où

. Écrivons alors, à l'aide du changement de
variables
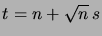
,
où nous avons posé
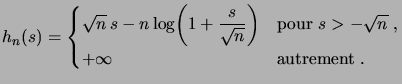 |
(1.22) |
Un développement limité en
montre que
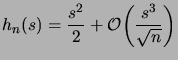 pour pour
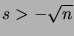 , , |
(1.23) |
et donc
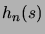
converge simplement vers
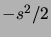
. D'autre part on
vérifie la minoration
 |
(1.24) |
valable pour tout
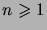
. On vérifie facilement que la fonction
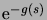
est intégrable. Par conséquent, le théorème de la
convergence dominée montre que l'on peut échanger limite

et intégrale, pour obtenir
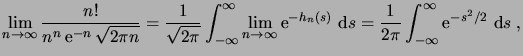 |
(1.25) |
et cette dernière intégrale vaut
par le lemme précédent.

Nous pouvons maintenant prouver le théorème de la limite
centrale pour la loi binomiale par un calcul relativement direct.
Rappelons que cette loi a espérance 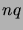 et variance
et variance 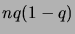 .
.
![\begin{theorem}[Moivre--Laplace]
Si $S_n$\ suit la loi binomiale de param\\lq etre ...
...{2\pi}}\,\6x
\end{equation}pour tout intervalle $[a,b]\subset\R$.
\end{theorem}](img162.png)
D´EMONSTRATION.
Nous allons considérer le cas
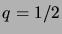
afin de simplifier les notations,
mais le cas d'un

quelconque se montre de manière totalement analogue.
Il s'agit de calculer
où
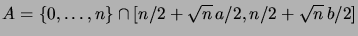
.
Dans la suite, nous dirons que deux fonctions
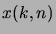
et
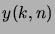
sont
équivalentes, et nous noterons
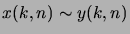
, si
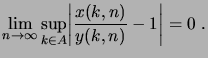 |
(1.27) |
En particulier, nous avons
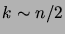
et
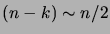
.
La formule de Stirling nous donne alors
Écrivons
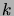
sous la forme
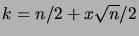
, avec
![$ x\in[a,b]$](img181.png)
. On aura
donc
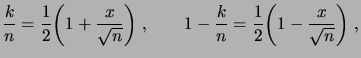 |
(1.29) |
et par conséquent
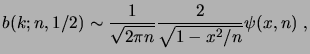 |
(1.30) |
où nous avons introduit
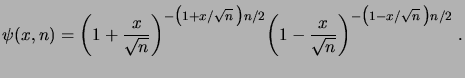 |
(1.31) |
Observons que le logarithme de
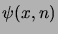
s'écrit
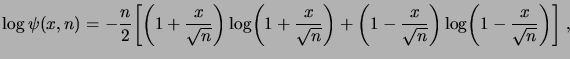 |
(1.32) |
et qu'un développement limité en
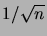
donne
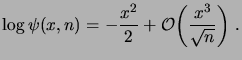 |
(1.33) |
Il suit donc de (
1.5.21) que
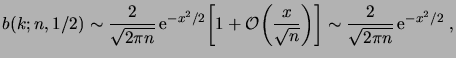 |
(1.34) |
puisque
![$ x\in[a,b]$](img181.png)
. En remplaçant dans (
1.5.17), il vient
 |
(1.35) |
La somme s'effectue sur des
régulièrement espacés de
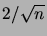
.
C'est donc une somme de Riemann, qui converge vers
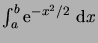
.

Nous donnons maintenant, sans démonstration, l'énoncé général du
théorème de la limite centrale.
![\begin{theorem}[Th\'eor\\lq eme de la limite centrale]
Soit $X_1, X_2, \dots$\ une ...
...= \int_a^b \frac{\e^{-x^2/2}}{\sqrt{2\pi}}\,\6x\;.
\end{equation}
\end{theorem}](img193.png)
![\begin{definition}[Loi normale]
La fonction
\begin{equation}
\Phi(x) = \int_{-\...
...tion}est appel\'ee la\/ \defwd{densit\'e de la loi normale}\/.
\end{definition}](img194.png)
Le Théorème 1.5.4 montre que pour 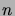 grand, on a
approximativement
grand, on a
approximativement
![$\displaystyle \biggprob{\frac{S_n-n\mu}{\sqrt{n\sigma^2}}\in[a,b]} \simeq \Phi(b) - \Phi(a)\;,$](img195.png) |
(1.36) |
ou encore
![$\displaystyle \bigprob{S_n\in[\hat a,\hat b]} \simeq \Phi\biggpar{\frac{\hat b ...
...u}{\sqrt{n\sigma^2}}} - \Phi\biggpar{\frac{\hat a - n\mu}{\sqrt{n\sigma^2}}}\;.$](img196.png) |
(1.37) |





Next: Loi de Poisson et
Up: Probabilités discrètes
Previous: Loi des grands nombres
Contents
berglund
2005-11-28
![]() de
de ![]() variables aléatoires de même espérance
variables aléatoires de même espérance
![]() et même variance
et même variance ![]() . Nous supposerons les
. Nous supposerons les ![]() indépendants. Nous avons vu dans la section précédente que la
moyenne
indépendants. Nous avons vu dans la section précédente que la
moyenne ![]() a une grande probabilité d'être proche de
a une grande probabilité d'être proche de ![]() , mais
comment se comporte l'écart
, mais
comment se comporte l'écart
![]() ? Dans la preuve du
Théorème 1.4.3, nous avons vu que
? Dans la preuve du
Théorème 1.4.3, nous avons vu que
![]() ,
,
![]() et variance
et variance ![]() .
.
![]() grand, on a
approximativement
grand, on a
approximativement