next up previous contents
Next: Chaînes de Markov ergodiques Up: Introduction aux processus stochastiques Previous: Les chaînes de Markov   Contents


Chaînes de Markov absorbantes


\begin{definition}[Cha\^\i ne de Markov absorbante]\hfill \begin{itemiz} \item U... ...i ne non absorbante est dite\/ \defwd{transiente}. \end{itemiz}\end{definition}

Il est commode de renuméroter les états d'une chaîne absorbante, en plaçant d'abord les états non absorbants, ensuite les états absorbants. Dans ce cas, on dira que la matrice de transition est écrite sous forme canonique

$\displaystyle P = \begin{pmatrix}Q & R \\ 0 & I \end{pmatrix}\;.$ (3.47)

S'il y a $ r$ états absorbants, $ Q$ est une matrice de taille $ (m-r)\times(m-r)$, $ R$ est une matrice de taille $ (m-r)\times r$ et $ I$ est la matrice identité de taille $ r$.


\begin{example} % latex2html id marker 3734Dans l'Exemple~\ref{ex_markov2} de ... ...trix} 1/2 & 0 \\ 0 & 0 \\ 0 & 1/2 \end{pmatrix}\;. \end{equation}\end{example}

Pour la matrice sous forme canonique (3.4.1), on vérifie facilement par récurrence que

$\displaystyle P^n = \begin{pmatrix}Q^n & \brak{I+Q+\dots+Q^{n-1}} R \\ 0 & I \end{pmatrix}\;.$ (3.48)

Pour comprendre le comportement à grand temps de la chaîne, il faut étudier l'évolution de cette matrice pour $ n\to\infty$.


\begin{prop} Pour une cha\^\i ne de Markov absorbante, \begin{equation} \lim_{n\to\infty} Q^n = 0\;. \end{equation}\end{prop}

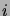
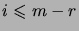
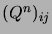
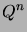
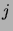
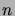
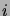
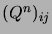
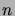
D´EMONSTRATION. Soit $ i$ un état non absorbant ( $ i\leqs m-r$). L'élément de matrice $ (Q^n)_{ij}$ de $ Q^n$ est la probabilité de se trouver dans l'état non absorbant $ j$, après $ n$ pas, partant de $ i$. Par conséquent, $ (Q^n)_{ij}$ est inférieur ou égal à la probabilité de ne par avoir atteint d'état absorbant en $ n$ pas. Soit

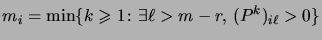$\displaystyle m_i = \min\setsuch{k\geqs1}{\exists \ell>m-r,\,(P^k)_{i\ell}>0}$ (3.49)

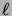
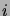
le nombre minimal de pas nécessaire à atteindre un état absorbant $ \ell$ depuis $ i$. Soit

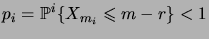$\displaystyle p_i = \probin{i}{X_{m_i}\leqs m-r} < 1$ (3.50)

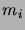
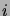
la probabilité de ne pas atteindre d'état absorbant en $ m_i$ pas, partant de $ i$. Soit enfin

$\displaystyle M = \max_{i=1,\dots,m-r} m_i\;, \qquad p = \max_{i=1,\dots,m-r} p_i\;.$ (3.51)

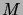
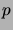
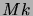
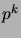
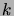
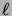
Alors la probabilité de ne pas atteindre d'état absorbant en $ M$ pas, partant de n'importe quel état non absorbant, est bornée par $ p$. Il suit que la probabilité de ne pas atteindre d'état absorbant en $ Mk$ pas est bornée par $ p^k$. Cette probabilité tend vers 0 lorsque $ k$ tend vers l'infini. 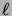La probabilité de ne pas être absorbé après un nombre arbitraire $ \ell$ de pas étant une fonction décroissante de $ \ell$, elle tend nécessairement vers 0. 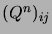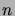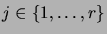Par conséquent, $ (Q^n)_{ij}$ tend vers zéro lorsque $ n$ tend vers l'infini, pour tout $ j\in\set{1,\dots,r}$. $ \qedsymbol$

Montrons maintenant que la matrice $ Q$ permet de déterminer le nombre moyen de passages dans chaque état non absorbant, avant de finir par atteindre un état absorbant.


\begin{theorem} Soit $P$\ la matrice de transition d'une cha\^\i ne de Markov ab... ...sum_{k\geqs0}\indexfct{X_k=j}}{X_0=i}\;. \end{equation}\end{enum} \end{theorem}

D´EMONSTRATION.
\begin{enum} \item Supposons que $x$\ soit un vecteur tel que $Qx=x$, c'est-\\lq a-... ...}Y_k} = \sum_{k\geqs0}(Q^k)_{ij} = (N)_{ij} = n_{ij}\;. \end{equation}\end{enum}
$ \qedsymbol$


\begin{definition}[Matrice fondamentale] $N$\ est appel\'ee la\/ \defwd{matrice fondamentale}\/ de la cha\^\i ne de matrice de transition $P$. \end{definition}

En utilisant les relations (3.4.5) et (3.4.9) dans l'expression (3.4.4) de $ P^n$, on obtient

$\displaystyle \lim_{n\to\infty }P^n = \begin{pmatrix}0 & N R \\ 0 & I \end{pmatrix}\;.$ (3.52)

La matrice $ NR$ devrait donc décrire les probabilités de transition d'un état non absorbant vers un état absorbant, en un nombre arbitraire de pas. Il nous reste également à caractériser le temps s'écoulant jusqu'à ce que le processus ait atteint un état absorbant. Son espérance peut aussi être déduite de la matrice $ N$.


\begin{theorem} Soit $N$\ la matrice fondamentale d'une cha\^\i ne de Markov abs... ... de la matrice \begin{equation} B = NR\;. \end{equation}\end{enum}\end{theorem}

D´EMONSTRATION.
\begin{enum} \item On a \begin{align} \nonumber \sum_{j=1}^{m-r} n_{ij} &= \sum... ...)_{iq} = (NR)_{iq}\;, \end{align}ce qui montre qu'on a bien $B=NR$. \end{enum}
$ \qedsymbol$


\begin{example} Rappelons que pour l'exemple de la marche de l'ivrogne, on a \b... ... les probabilit\'es respectives de finir au bar ou \\lq a la maison. \end{example}

next up previous contents
Next: Chaînes de Markov ergodiques Up: Introduction aux processus stochastiques Previous: Les chaînes de Markov   Contents
berglund 2005-11-28