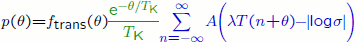
Cycling

The distribution of first-exit locations through an unstable periodic orbit of a planar system, subjected to additive white noise. See here for more details.

The expression we use in the animations below is

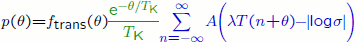
where

• the transient factor f_trans(t) is only present when the system does not start in its quasistationary distribution; it increases from 0 to 1 in a time of order |log σ|, where σ is the noise intensity;
• the exponential term decays on a timescale T_K(σ) = e^H/σ2 related to Kramers' time, where H is the quasipotential;
• the periodic part is a universal function (for a suitable parametrization θ of the periodic orbit) of period equal to the orbit's period T times its Lyapunov exponent λ. The function

  

  is the density of a type-1 Gumbel distribution with mode -log 2/2 and scale parameter 1/2.

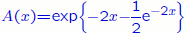
The following animation shows how the exit distribution changes as the noise intensity σ decreases from 1 to 0.0001. The system starts in its quasistationary distribution, in order to avoid transients which become longer as the noise intensity decreases. Parameter values are: Lyapunov exponent λ=1, quasipotential H=1 and period T=4. The distribution has been normalised so that the maximum, not the area under the curve, is constant.

A full resolution version of the animation is here (AVI, 22Mb).

The following animation shows how the exit distribution changes as the orbit's period increases from 0.001 times Kramers' time to 5 times Kramers' time. Parameter values are: Lyapunov exponent λ=1, quasipotential H=1 and noise intensity σ=0.4. The distribution has been normalised so that the maximum, not the area under the curve, is constant.

A full resolution version of the animation is here (AVI, 13Mb).

The link with residence-time distributions for stochastic resonance is explained here.

Top

Home