
Stochastic resonance and noise-induced synchronization
Stochastic resonance is a mechanism where additive noise enhances the response of a bistable system to a weak periodic driving signal. It was initially introduced as a model to explain the occurence of ice ages, and has been observed in various physical and biological systems. When the noise intensity is sufficiently large to produce close-to-periodic oscillations in the system's response, one also speaks of noise-induced synchronization.
These phenomena can be observed in the overdamped motion of a particle in a periodically modulated double-well potential, subject to additive white noise. Here is an animation of the phenomenon:
We have considered two classes of potentials, asymmetric and symmetric ones. The results are discussed in this paper. In this subsequent work, we have determined the residence-time distribution of the system, that is, the law of the time elapsing between transitions from one well to another. This law is given by an exponential modulated by a universal periodic function.
A typical example of equation describing the motion in an asymmetric potential is

If A is smaller than a critical value, transitions between potential wells are impossible when σ = 0. On the other hand, if σ > 0 and A = 0, noise will cause the particle to jump from one well to the other one at random times. If both parameters A and σ are positive, however, and suitably tuned, solutions will jump from one well to the other one in a close to periodic way, a phenomenon known as synchronization.
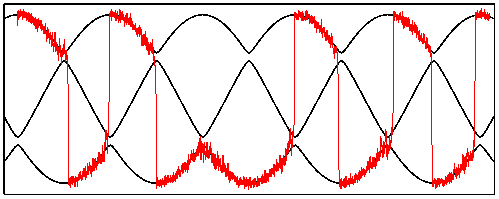
A typical sample path of the above stochastic differential equation with asymmetric potential, as a function of slow time εt. The upper and lower black curve are the locations of potential wells, while the middle curve indicates the location of the saddle. When the noise intensity is large enough, the path is likely to overcome the potential barrier near the instant when it reaches minimal height.
We show the existence of a threshold for the noise intensity σ, depending on ε and the minimal barrier height. Below the threshold, paths have an exponentially small probability to jump from one well to the other one. Above the threshold, they do jump with probability exponentially close to one, with an exponent of order σ4/3/ε. The transition zones have a width in (slow) time of order σ2/3.
A typical example of equation describing the motion in a symmetric potential is
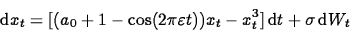
where a0 is a positive small parameter controlling the minimal barrier height. As in the asymmetric case, there is a threshold value for σ such that transitions are unlikely below the threshold. For sufficiently large noise intensity, transitions occur with a probability exponentially close to 1/2, with an exponent of order σ3/2/ε. The transition zones have a width in (slow) time of order σ1/2.
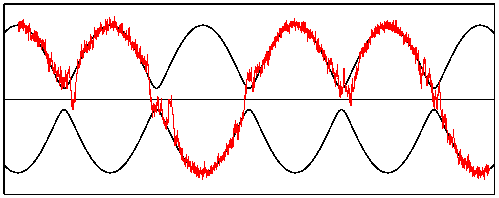
A typical sample path of the above stochastic differential equation with asymmetric potential, as a function of slow time εt. The upper and lower black curve are the locations of potential wells, while the straight line indicates the location of the saddle. When the noise intensity is large enough, the particle overcomes the potential barrier near the instant when it is lowest, with a probability close to 1/2.
The residence time is the random time span spent inside a potential well between two successive interwell transitions. Using results on first-passage times through unstable periodic orbits (see here and here, as well as these animations), we have shown here that this distribution's density is approximately
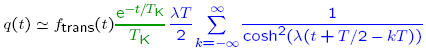
where
Here is an animation showing how the distribution changes as the period increases from 0.001TK to 5TK: