Main results

In this work, we consider mainly adiabatic differential equations of the form

εdx/dτ = F(x,λ(τ)),

where x is the vector of dynamic variables, τ = εt is the slow time, ε the small adiabatic parameter, and λ(τ) the slowly varying parameter. The main idea is to establish connections between solutions of this equation and those of the associated family of frozen dynamical systems dx/dt = F(x,λ).

Detailed results are contained in my Ph.D. thesis, and a summary of mathematical results can be found in this proceedings. A non-technical description is given here, several physical applications are found in this paper, while chaotic hysteresis is briefly described in this letter.

• Adiabatic solutions: If x*(λ) is a hyperbolic equilibrium branch of F(x, λ), we show the existence of a particular solution of the adiabatic system, which tracks the branch at a distance of order ε. We call it an adiabatic solution. It can be expanded in a power series of the adiabatic parameter ε. Even when the function F is analytic, this series does not converge in general, but can be truncated at exponentially small order.

• Bifurcations: Assume x is a scalar variable, and the origin is a bifurcation point of f(x,τ) = F(x, λ(τ)). If x*(τ) is an equilibrium branch arriving at the origin, adiabatic solutions no longer track this branch at a distance of order ε, but at a distance scaling with some other power of ε. We developed a method to compute this exponent in a simple way, using Newton's polygon. It allows to determine scaling laws of hysteresis cycles in an easy, geometric way. In the vectorial case, the same method can be applied after using a centre manifold reduction.

• Linear systems: When linearized around an adiabatic solution, the adiabatic system takes the form ε dx/dτ= A(τ)x. We provide a method to diagonalize this equation dynamically, when its eigenvalues have different real parts. Eigenvalue crossings can be studied by a local analysis. In some cases, these crossings lead to a similar behaviour than bifurcations.

• Invariant manifolds: Adiabatic solutions tracking a hyperbolic equilibrium admit stable and unstable invariant manifolds. We showed that in a neighbourhood of the branch, they can be represented by graphs, admitting power series in ε. In the analytic case, they can be truncated to exponentially small order.

• Dynamic normal forms: Another way to simplify a nonlinear equation of the form εdx/dτ = A(τ)x + b(x,τ), is to try to eliminate the nonlinear term b by a change of variables. This turns out to be possible in the nonresonant case. Resonant terms can be dealed with by a local analysis, which is again similar to the analysis of bifurcations.

• Chaotic hysteresis: Consider a damped pendulum on a table, rotating with a slowly modulated angular frequency. When the frequency is small, the downward position of the pendulum is stable. When the frequency is sufficiently high, this position becomes unstable, and the pendulum makes an angle with the vertical. When the frequency is modulated periodically, the system displays hysteresis: the pendulum leaves the vertical position at a frequency which is higher than when he drops back. Moreover, the pendulum does not always choose the same asymmetric equilibrium: for some values of the parameter, it may visit these positions in a chaotic sequence. We explain this behaviour by computing an asymptotic expression for the Poincaré map, using the methods described above (see this letter).

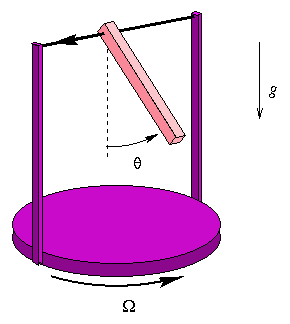
The rotating pendulum is mounted on a table rotating with angular frequency Ω. It experiences friction, gravity and an intertial torque. When the frequency Ω is varied periodically, this system sometimes displays chaotic hysteresis: each time the frequency becomes large, the pendulum leaves the origin for one of two possible equilibria at an angle. The sequence of visited equilibria is chaotic for some values of the parameters.

• Magnetic hysteresis: Consider a lattice system with infinite range interaction (Curie-Weiss model), and Glauber spin flip dynamics. Its magnetization obeys an effective mean field equation. We studied this equation for one- and two-dimensional spins and a periodically varying magnetic field, in order to investigate the mechanism of magnetization reversal, dynamic phase transitions, and the shape and area of hysteresis cycles.